Changing Area and Faraday’s Law

Consider the classic introductory problem where a bar is moving over a constant magnetic field. What is the generated EMF \(\varepsilon\)?

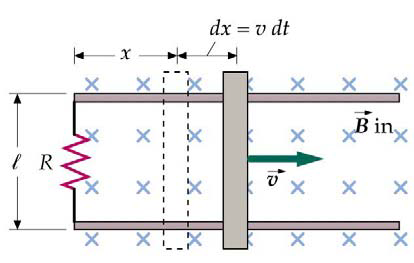
The Standard Solution

Using Maxwell’s equations and Lenz’s law, EMF is given as \(\varepsilon = - \frac{d\Phi}{dt}\)
where \(\Phi=\int B\cdot dA=BA\). Because \(B\) is constant and the area is changing we get that

\[\boxed{\varepsilon = -\ell B v }\]

Less Obvious Solution

Looking at Maxwell’s equations we have

\[\nabla \times E= - \frac{\partial B}{\partial t}\]

However, \(\frac{\partial B}{\partial t}=0\), which seems to imply \(E=0\) here! To rectify this, we notice that it implies the electric field is a constant not zero, which makes sense given the EMF given above. It’s also important to notice that you cannot move the time derivative past the integral sign without the chain rule, as the area part of the integral is time dependent.